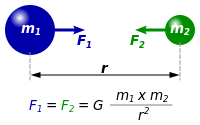
กฎความโน้มถ่วงสากลของนิวตัน

กฎความโน้มถ่วงสากลของนิวตัน (อังกฤษ: Newton's law of universal gravitation) ระบุว่า แต่ละจุดมวลในเอกภพจะดึงดูดจุดมวลอื่นๆ ด้วยแรงที่มีขนาดเป็นสัดส่วนโดยตรงกับผลคูณของมวลทั้งสอง และเป็นสัดส่วนผกผันกับค่ากำลังสองของระยะห่างระหว่างกัน นี่คือกฎฟิสิกส์ทั่วไปที่ได้จากการสังเกตการณ์ของไอแซก นิวตัน เป็นส่วนหนึ่งของกลศาสตร์ดั้งเดิม และเป็นส่วนสำคัญอยู่ในงานของนิวตันชื่อ Philosophiae Naturalis Principia Mathematica ("the Principia") ซึ่งเผยแพร่ครั้งแรกเมื่อวันที่ 5 กรกฎาคม ค.ศ. 1687

ศาสตราจารย์วอลเตอร์ เลวิน (Prof. Walter Lewin) กำลังอธิบายกฎแรงโน้มถ่วงสากลของนิวตันในหลักสูตร 8.01 ที่สถาบันเอ็มไอที (MIT course 8.01 เก็บถาวร 2012-10-28 ที่ เวย์แบ็กแมชชีน)

ดาวเทียมและกระสุนปืนทั้งหมดล้วนแล้วแต่เป็นไปตามกฏแห่งแรงโน้มถ่วงของนิวตันทั้งสิ้น

กฎดังกล่าวแสดงเป็นสมการได้ดังนี้

$F=G{\frac {m_{1}m_{2}}{r^{2}}}\$,

โดยที่:

• F คือแรงดึงดูดระหว่างมวล,
• G คือ ค่าคงที่โน้มถ่วงสากล,
• m₁ คือมวลก้อนแรก,
• m₂ คือมวลก้อนที่สอง, และ
• r คือระยะห่างระหว่างมวล

สมมติว่าระบบเอสไอ (SI units), F มีหน่วยวัดเป็นนิวตัน (N), m₁ และ m₂ เป็นกิโลกรัม (kg), r ในหน่วยเมตร (m) และ ค่าคงที่ G จะประมาณเท่ากับ 6.674×10⁻¹¹ นิวตัน เมตร² กิโลกรัม⁻² ค่าคงที่ G เป็นค่าที่ถูกกำหนดได้อย่างถูกต้องเป็นครั้งแรกจากผลการทดลองของคาเวนดิช (Cavendish experiment) ที่ดำเนินการโดย เฮนรี คาเวนดิช นักวิทยาศาสตร์ชาวอังกฤษในปี ค.ศ. 1798, แม้ว่าคาเวนดิชจะไม่ได้คำนวณค่าเชิงตัวเลข G ด้วยตัวของเขาเองก็ตาม การทดลองครั้งนี้ยังเป็นครั้งแรกของการทดสอบทฤษฎีของนิวตันของความโน้มถ่วงระหว่างมวลในห้องปฏิบัติการอีกด้วย มันเกิดขึ้นหลังจากเวลาผ่านไป 111 ปี หลังจากการประกาศตีพิมพ์คัมภีร์ Principia ของนิวตันและ 71 ปีหลังจากการตายของนิวตัน, จึงยังไม่มีใครสามารถทำการคำนวณสมการของนิวตันให้สามารถใช้ค่าของ G; ได้แทนเขา ซึ่งมีแต่เขาผู้เดียวเท่านั้นที่สามารถคำนวณแรงที่สัมพันธ์กับแรงอื่น ๆ ได้

กฎของความโน้มถ่วงของนิวตันมีลักษณะคล้ายกฏของคูลอมบ์ (Coulomb's law) ของแรงทางไฟฟ้า, ซึ่งจะใช้ในการคำนวณหาขนาดของแรงทางไฟฟ้าที่เกิดขึ้นระหว่างวัตถุที่มีประจุไฟฟ้าสองก้อน กฎทั้งสองนี้ ต่างก็เป็น "กฏกำลังสองผกผัน" (inverse-square laws) ที่แรงจะเป็นสัดส่วนผกผันกับกำลังสองของระยะห่างระหว่างวัตถุ

กฎของนิวตันถูกแทนที่ด้วยทฤษฎีสัมพัทธภาพทั่วไปของอัลเบิร์ต ไอน์สไตน์ แต่ยังใช้เป็นการประมาณค่าที่ยอดเยี่ยมของผลแห่งความโน้มถ่วงในการประยุกต์ส่วนใหญ่ จำเป็นต้องใช้สัมพัทธภาพเฉพาะเมื่อมีความจำเป็นสำหรับความแม่นยำอย่างยิ่งเท่านั้น หรือเมื่อจัดการกับสนามความโน้มถ่วงที่เข้มจัด เช่น สนามความโน้มถ่วงที่พบใกล้กับวัตถุที่มีขนาดใหญ่และหนาแน่นอย่างยิ่ง หรือที่ระยะใกล้มาก (เช่นวงโคจรของดาวพุธรอบดวงอาทิตย์)

รูปแบบเวกเตอร์

เส้นสนามถูกลากเส้นสำหรับจุดมวลโดยใช้เส้นสนาม 24 เส้น

สนามแรงโน้มถ่วงรอบโลกจากมุมมองด้วยตาเปล่า

กฎความโน้มถ่วงสากลสามารถเขียนเป็นสมการเวกเตอร์ (vector equation) เพื่ออธิบายสำหรับทิศทางของแรงโน้มถ่วงเช่นเดียวกับขนาดของมัน ในสูตรนี้ปริมาณที่เป็นตัวหนาเป็นตัวแทนของเวกเตอร์

$\mathbf {F} _{21}=-G{m_{1}m_{2} \over {\vert \mathbf {r} _{12}\vert }^{2}}\,\mathbf {\hat {r}} _{12}$

where

F₁₂ คือแรงที่ถูกนำมาประยุกต์ใช้ในวัตถุที่ 2 อันเนื่องมาจากวัตถุที่ 1,

G คือ ค่าคงที่โน้มถ่วงสากล (gravitational constant),

m₁ และ m₂ คือ มวลของวัตถุที่ 1 และ 2 ตามลำดับ,

|r₁₂| = |r₂ − r₁| คือ ระยะทางระหว่างวัตถุที่ 1 และ 2 และ

$\mathbf {\hat {r}} _{12}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathbf {r} _{2}-\mathbf {r} _{1}}{\vert \mathbf {r} _{2}-\mathbf {r} _{1}\vert }}$ คือ เวกเตอร์หนึ่งหน่วย (unit vector) จากวัตถุที่ 1 ถึง วัตถุที่ 2